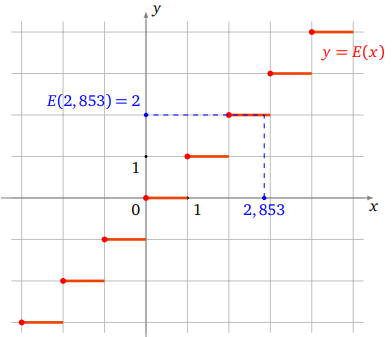
Soit un entier \(N\geqslant1\)
Montrer que pour tout entier \(n\) vérifiant \(N^2+1\leqslant n\leqslant N^2+2N\), on a : $$E(\sqrt n)=N$$

Passer l'inégalité à la racine carrée
La fonction \(x\mapsto\sqrt x\) est strictement croissante sur \(]0,+\infty[\), on a donc : $$\sqrt{N^2+1}\leqslant\sqrt n\leqslant\sqrt{N^2+2N}$$

Majoration et minoration de l'encadrement
$$\implies\sqrt{N^2}\lt \sqrt n\lt \sqrt{N^2+2N+1}$$

Simplification
$$\implies N\lt \sqrt n\lt N+1\implies N\leqslant\sqrt n\lt N+1$$

On a donc \(E(\sqrt n)=N\) d'après la définition de la partie entière

(Racine carrée, [[]])